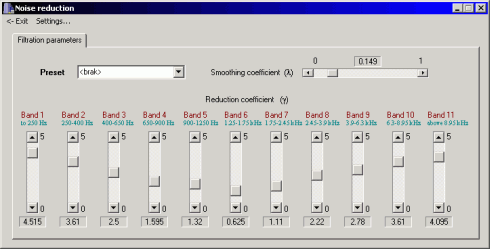
Noise reduction

The background noise is the most common factor degrading the quality and intelligibility of speech in recordings. The noise reduction module intends to lower the noise level without affecting the speech signal quality. This module is based on the spectral subtraction performed independently in the frequency bands corresponding to the auditory critical bands.

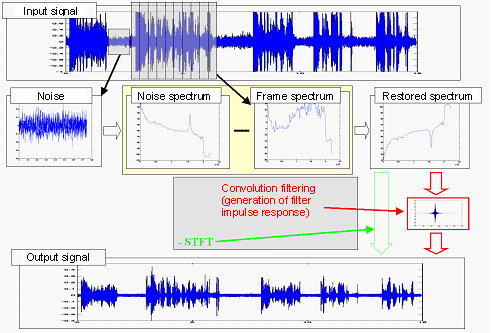
The spectral subtraction method is a simple and effective method of noise reduction. In this method, an average signal spectrum and average noise spectrum are estimated in parts of the recording and subtracted from each other, so that average signal-to-noise ratio (SNR) is improved. It is assumed that the signal is distorted by a wide-band, stationary, additive noise, the noise estimate is the same during the analysis and the restoration and the phase is the same in the original and restored signal.

The noisy signal y(m) is a sum of the desired signal x(m) and the noise n(m):

y(m) = x(m) + n(m)

In the frequency domain, this may be denoted as:

Y(jω) = X(jω) + N(jω)  =>  X(jω) = Y(jω) - N(jω)

where Y(jω), X(jω), N(jω) are Fourier transforms of y(m), x(m), n(m), respectively.

The statistic parameters of the noise are not known, thus the noise and the speech signal are replaced by their estimates:

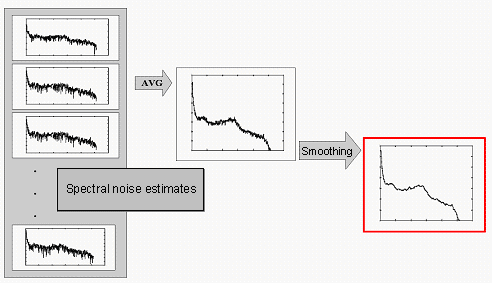
The noise spectrum estimate is related to the expected noise spectrum which is usually calculated using the time-averaged noise spectrum taken from parts of the recording where only noise is present. The noise estimate is given by:

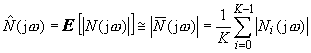
where is the amplitude spectrum of the i-th of the K frames of noise. Noise estimate in k-th frame may be obtained by filtering the noise using first-order low-pass filter:

where is the smoothed noise estimate in i-th frame, λ_n is the filtering coefficient (0.5 ≤ λ_n ≤ 0.9, some authors use values 0.8 ≤ λ_n ≤ 0.95). To obtain the noise estimate, the part of the recording containing only noise that precedes the part containing speech signal should be analysed (the length of the analysed fragment should be at least 300 ms). To achieve this, additional speech detector has to be used.

The spectral subtraction error may be defined as:

This error degrades the signal quality, introducing the distortion known as residual noise or musical noise. The error is a function of expected or average noise spectrum estimate:

.

Therefore, the longer noise section is used in analysis, the more accurate the noise estimate is.

The signal-to-noise ratio may be defined in frequency domain as SNR a priori (for clean signal) or SNR a posteriori (for noisy signal). SNR in k-th frame is given by:

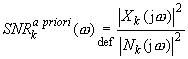
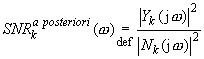
During the restoration process, the clean signal is not known, hence the SNR a priori value has to be estimated. Using the Gaussian model, optimal SNR in k-th frame may be defined as:

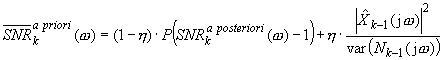
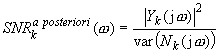
where P(x) is:

,

is the variance of the noise spectrum in the previous frame, is estimate of the restored signal and η is constant (0.9 < η < 0.98). The variance is usually replaced by spectral power of noise estimate:

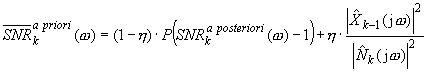
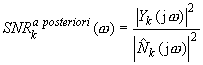
Calculation of the averaged noise estimate

Spectral subtraction method

Before the restoration process is started, a part of the recording containing only noise (not shorter than 1 second) has to be selected in the main window of the Restorer application. The window of the noise reduction module enables user to set reduction coefficient γ in each of the 11 frequency bands and the smoothing coefficient λ. It is recommended to start the processing by setting all reduction coefficients to the middle value. During the restoration, the reduction coefficients should be reduced in bands where the speech signal becomes distorted and increased in the bands where noise level is too high.