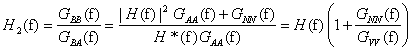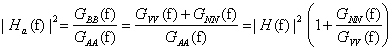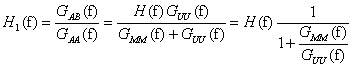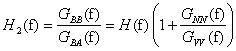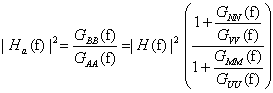Dwukanałowe analizotory FFT
Na tej stronie zostały przedstawione podstawy teoretyczne technik pomiarów dwukanałowymi analizatorami FFT.
Głównym zadaniem tego typu analizatorów jest mierzenie relacji pomiędzy wejściem, a wyjściem urządzenia. Zakładając,
że badane urządzenie jest liniowe potrafią one obliczyć funkcję opisującą jego dynamiczne zachowanie, czyli potrafią
przewidzieć, co pojawi się na wyjściu danego urządzenia mając dany sygnał wejściowy lub obliczyć sygnał wejściowy,
który spowoduje określoną odpowiedź urządzenia.
Zobacz przykładowe funkcje dwukanałowego analizatora firmy B&K
Podstawy teoretyczne

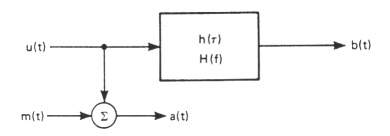
Powyższy rysunek przedstawia funkcje opisujące badany system, czyli pobudzenie a(t), odpowiedź b(t) oraz odpowiadające im w dziedzinie częstotliwości A(f) oraz B(f).
Funkcja opisująca urządzenie w dziedzinie czasu nosi nazwę odpowiedzi impulsowej h(τ), a w dziedzinie
częstotliwości odpowiedzi częstotliwościowej H(f). Te dwie wielkości opisują zależności miedzy pobudzeniem, a
odpowiedzią urządzenia w sposób opisany wzorami:
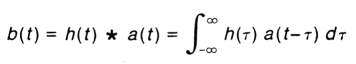
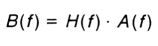
Pomiary dwukanałowe dają możliwość eliminacji błędu wprowadzanego przez szumy i inne zakłócenia. Obliczenie widma skrośnego pozwala na określenie opóźnienia pomiędzy dwoma wyjściami badanego systemu.
Pomiar dwukanałowy opiera się na obliczeniu widma skrośnego sygnałów w kanałach oraz widma mocy dla każdego z kanałów, wszystkie pozostałe funkcje realizowane są korzystając z tych trzech widm.

Schemat blokowy analizatora dwukanałowego
Przebiegi czasowe w kanałach zostają wpierw przeniesione w dziedzinę częstotliwości poprzez zastosowanie transformaty Fouriera:
Widmo mocy obliczane jest dla kanału A według wzoru
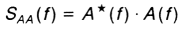
odpowiednio dla kanału B według wzoru
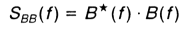
natomiast widmo skrośne według wzoru
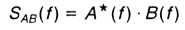
* oznacza sprzężenie
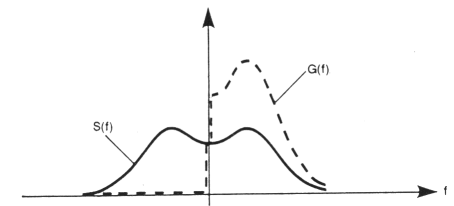
Ponieważ widma te cechuje symetryczność, czyli informacja dla częstotliwości ujemnych jest taka sama jak dla
częstotliwości dodatnich, dla wygody obliczeń stosuje się odpowiadające im widma jednostronne tworzone według
poniższych wzorów
Poniższy wykres przedstawia widmo jednostronne G(f) utworzone z widma dwustronnego S(f)
Podczas analizy systemu, gdy mierzone jest wejście i wyjście bardzo ważną rzeczą jest określenie stopnia liniowości
pomiędzy nimi. Mając dane dwie zmienne x oraz y odpowiadające wejściu i wyjściu systemu obliczamy współczynnik
korelacji między nimi ρxy zdefiniowany wzorem
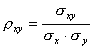
gdzie σxy jest kowariancją x oraz y daną wzorem 
natomiast σx oraz σy są odchyleniami standardowymi 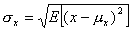
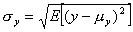
E oznacza wartość oczekiwaną, natomiast µx oraz µy są wartościami średnimi x oraz odpowiednio y, czyli np.
µx=E[x]; µy=E[y]
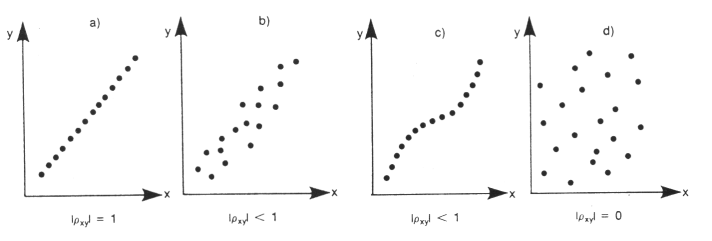
Jeśli x oraz y są dla wszystkich próbek związane ze sobą funkcją idealnie liniową (y=αx+β), wtedy |ρxy| będzie
wynosić dokładnie 1 (wykres "a"). Jeśli system jest liniowy, ale próbki zawierają w sobie pewną ilość przypadkowego
szumu, wtedy |ρxy| będzie miało wartość mniejszą niż 1 (wykres "b"), |ρxy| będzie posiadało wartość mniejszą od 1
także w przypadku, gdy system będzie nieliniowy (wykres "c"). Jeśli natomiast próbki x oraz y będą zupełnie ze sobą
niepowiązane, wtedy współczynnik korelacji wyniesie zero (wykres "d"). Jak więc widać współczynnik korelacji ρxy
może być miarą liniowości zależności pomiędzy dwoma zmiennymi x oraz y.
Kolejną funkcją możliwą do policzenia przy pomiarach dwukanałowych jest koherencja γ2(f) wyrażona wzorem
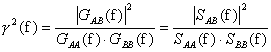
Dla każdej częstotliwości koherencja odpowiada współczynnikowi korelacji podniesionemu do kwadratu.

Dlatego koherencja γ2(f) podobnie jak współczynnik korelacji jest funkcją, która w skali od 0 do 1
określa stopień liniowości pomiędzy dwoma sygnałami a(t) i b(t) dla danej częstotliwości f.
Dodatkowym powodem koherencji mniejszej od 1 może być nieuwzględnienie w analizie opóźnień między sygnałami.
Najczęstszą przyczyną stosowania analizy dwukanałowej jest chęć wyznaczenia funkcji H(f) określającej charakterystykę
częstotliwościową urządzenia zdefiniowaną wzorem  .
.
Przed rozpoczęciem wyznaczania funkcji H(f) należy przyjąć pewne założenia. Badany system musi być:
- przyczynowy: h(τ) = 0 dla τ < 0.
- stacjonarny: h(τ,t) = h(τ) oraz H(f,t) = H(f), -oo< t <oo.
- stabilny:
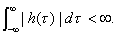
- liniowy: jeżeli pobudzenie a1(t) powoduje odpowiedź b1(t)
a1(t) => b1(t) oraz a2(t) => b2(t), wtedy
a1(t) + a2(t) => b1(t) + b2(t) oraz
c · a1(t) => c · b1(t).
Wychodząc z fundamentalnej zależności B(f)=H(f)·A(f) (*), mnożąc obydwie strony równania przez A*(f)
A*(f)·B(f) = H(f)·A*(f)·A(f)
SAB(f) = H(f)·SAA(f)
zamieniając widma dwustronne S(f) na jednostronne G(f) otrzymujemy wzór
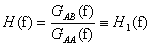
określający funkcję charakterystyki częstotliwościowej, oznaczoną jako H1(f).
Postępując podobnie jednak tym razem mnożąc obydwie strony równania (*) przez B*(f) otrzymamy wzór definiujący nam funkcje H2(f).

W praktyce najczęściej H1(f) różni się od H2(f).
Korzystając z faktu, iż  możemy zapisać równość:
możemy zapisać równość:

Równanie (*) można także przekształcić podnosząc je do kwadratu
B*(f)·B(f) = H*(f)·H(f) · A*(f)·A(f)
SBB(f) = |H(f)|2 · SAA(f)
GBB(f) = |H(f)|2 · GAA(f)
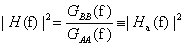
Powyższy wzór definiuje trzeci typ charakterystyki częstotliwościowej Ha(f).
W dalszej części zostanie przedyskutowane zastosowanie zdefiniowanych wyżej typów charakterystyk częstotliwościowych w
zależności od rodzaju zakłóceń występujących w systemie.
1. System idealny

Rozpatrując przypadek idealny, w którym badane sygnały są pozbawione jakichkolwiek zakłóceń, prawdziwe są równości
H1(f) = H2(f) = H(f) oraz |Ha(f)| = |H(f)|.
2. System z szumem w sygnale wyjściowym

W przypadku, gdy w sygnale wyjściowym znajdują się zakłócenia w postaci szumu n(t) nieskorelowanego z sygnałem
wejściowym a(t), czyli GAN(f) = GVN(f) = 0, możemy zapisać następujące równości
GBB(f) = GVV(f) + GNN(f) = |H(f)|2 GAA(f) + GNN(f)
GAB(f) = GAV(f) + GAN(f) = GAV(f) = H(f) GAA(f)
Jak widać powyżej widmo skrośne jest w tym przypadku pozbawione błędów spowodowanych przez dodatkowe źródło
szumu w systemie, dlatego też charakterystykę częstotliwościową najlepiej jest wyznaczać w tym przypadku z wzoru
na H1(f).
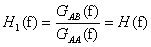
Estymata H2(f) da w tym przypadku wynik zafałszowany, ponieważ do jej wyliczenia zostanie użyty także
czynnik szumowy GNN(f).
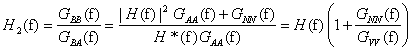
Estymata metodą autospektrum Ha również będzie zafałszowana.
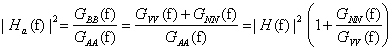
3. System z szumem w sygnale wejściowym
Rozpatrując analogiczną sytuacje, w której jednak zakłócenia m(t) występują w sygnale wejściowym otrzymujemy
następujące równania
GAA(f) = GMM(f) + GUU(f)
GBB(f) = |H(f)|2 GUU(f) + GNN(f) = |H(f)|2 (GAA(f)-GMM(f))
GAB(f) = GUB(f) = H(f) GUU(f)
oraz następujące estymaty charakterystyk częstotliwościowych
Jak wynika z powyższych wyliczeń, w tym przypadku estymata H2(f) jest niewrażliwa na szum na wejściu układu pomiarowego.
4. System z szumem w sygnale wejściowym oraz wyjściowym
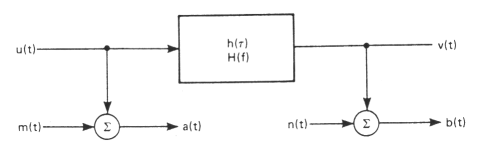
W przypadku, gdy zakłócenia będą występowały zarówno w sygnale wejściowym jak i wyjściowym, odpowiednie wielkości
będą opisane poniższymi wzorami.
| |
GAA(f) = GMM(f) + GUU(f)
GBB(f) = |H(f)|2 GUU(f) + GNN(f) = |H(f)|2 (GAA(f)-GMM(f))
GAB(f) = GUB(f) = H(f) GUU(f)
|
|
| |

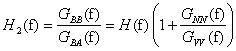
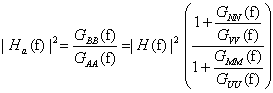
|
Jak widać |H1(f)| będzie zaniżona z powodu szumu na wejściu, |H2(f)| będzie zawyżona z powodu
szumu na wyjściu, natomiast |Ha(f)| będzie mniejsza, większa lub równa |H(f)| w zależności od stosunków
sygnałów GNN(f)/GVV(f) oraz GMM(f)/GUU(f).
 Dwukanałowe analizatory FFT - Quiz
Dwukanałowe analizatory FFT - Quiz



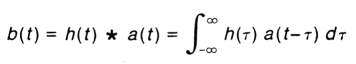
![]()


![]()

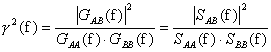

![]()
![]()
![]()
![]()


![]()