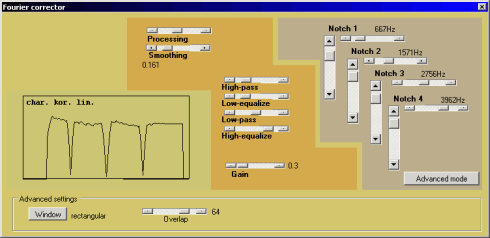
Fourier corrector

The aim of the Fourier corrector module is to modify the signal spectrum in order to make it similar to the reference speech pattern (speech signal recorded in good acoustic conditions) and to remove distortions using the digital filters. Average spectrum of the pattern is computed using the spectrum analyser module and saved to a disk. The Fourier corrector module computes average spectrum of the recording and correction function is determined by dividing both average spectra:

where v_i(n) is corrected i-th signal segment, x_i(n) - original i-th signal segment, s(n) - average speech pattern spectrum, x(n) - average signal spectrum.

This algorithm is similar to the blind deconvolution method, but additional parameters may be set by the user. Correction factor (0%-100%) is the degree to which the signal is modified by the algorithm. Smoothing factor (0.001-1) is related to the modification of the correction function maxima (e.g. sharp peaks). The algorithm may be described using the equation:

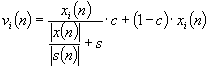
where c is correction factor and s is smoothing factor.

The filtering algorithm is implemented in the Fourier bands, linearly spaced in the frequency range (the distance between each two adjacent Fourier bands is ca. 21.53 Hz). Five filtering methods are available:

• high-pass: v_i(n) = 0 for 0 ≤ n ≤ p
• low-pass: v_i(n) = 0 for p ≤ n ≤ N
• low-equalize: v_i(n) = v_i(p) for 0 ≤ n ≤ p
• high-equalize: v_i(n) = v_i(p) for p ≤ n ≤ N
• notch:

  

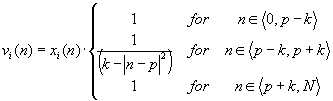
  where p is the number of the 'cut-off' Fourier band, N is the number of the Fourier band for the Nyquist frequency, k - attenuation coefficient. Four notch filters are available.

Additional parameters that may be set by the user are time windowing function and amount of overlapping between signal sections in analysis. The shape of the correction function, including the filtering options, is presented in the plot. The plot is automatically updated after any change of the parameters.